「Mac玩转仓颉内测版50」小学奥数篇13 - 动态规划入门

本篇将通过 Python 和 Cangjie 双语介绍动态规划的基本概念，并解决一个经典问题：斐波那契数列。学生将学习如何使用动态规划优化递归计算，并掌握编程中的重要算法思想。

---

关键词

• 小学奥数
• Python + Cangjie
• 动态规划
• 斐波那契数列

---

一、题目描述

斐波那契数列的定义如下：

• F(0) = 0, F(1) = 1
• F(n) = F(n-1) + F(n-2)（当 n ≥ 2）

请编写程序，接收一个非负整数 n，并输出 F(n) 的值。要求使用动态规划解决问题，以避免重复计算。

输入格式：

• 一个非负整数 n。

输出格式：

• 输出 F(n) 的值。

---

解题思路

1. 递归问题的优化：普通递归会导致大量重复计算。使用动态规划将计算结果存储起来，避免重复运算。
2. 动态规划实现方式：采用自底向上的方式，逐步计算每个状态的结果。

---

二、Python 实现

import matplotlib.pyplot as plt

# 计算斐波那契数列的第 n 项
def fibonacci(n):
    dp = [0] * (n + 1)  # 初始化数组
    if n > 0:
        dp[1] = 1

    for i in range(2, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]

    return dp[n], dp  # 返回结果和完整序列

# 绘制斐波那契数列的图像并保存
def plot_fibonacci_sequence(n):
    _, sequence = fibonacci(n)
    plt.plot(range(n + 1), sequence, marker='o')
    plt.title(f"斐波那契数列前 {n} 项")
    plt.xlabel("n")
    plt.ylabel("F(n)")
    plt.grid(True)
    filename = "fibonacci_sequence.png"
    plt.savefig(filename)  # 保存图像到本地
    print(f"图形已保存为 {filename}")
    plt.show()

# 输入并计算
n = int(input("请输入一个非负整数 n: "))
result, _ = fibonacci(n)
print(f"F({n}) = {result}")

plot_fibonacci_sequence(n)  # 绘制并保存图像

---

三、Cangjie 实现

package cjcDemo

// 导入必要的标准库模块
import std.convert.*    // 数据类型转换模块
import std.console.*    // 控制台输入输出模块

// 定义一个函数，读取用户输入的整数，并返回 Int64 类型的值
func inputInt(info: String): Int64 {
    print(info)  // 输出提示信息到控制台
    let number: Int64 = Int64.parse(Console.stdIn.readln().getOrThrow())  // 读取用户输入并转换为 Int64
    return number  // 返回输入的整数
}

// 计算斐波那契数列的第 n 项，并返回该项的值及完整数列
func fibonacci(n: Int64): (Int64, Array<Int64>) {
    // 创建一个大小为 n+1 的数组，用于存储斐波那契数列的各项，初始化为 0
    let dp = Array<Int64>(n + 1, repeat: 0)
    
    // 如果 n 大于 0，则设置第一项为 1（F(1) = 1）
    if (n > 0) {
        dp[1] = 1
    }

    // 使用循环计算斐波那契数列的每一项，避免重复计算
    for (i in 2..=n) {
        dp[i] = dp[i - 1] + dp[i - 2]  // 当前项为前两项之和
    }

    // 返回第 n 项的值和完整的斐波那契数列数组
    return (dp[n], dp)
}

// 主函数，程序入口
main(): Int64 {
    // 调用 inputInt 函数，提示用户输入非负整数 n
    let n = inputInt("请输入一个非负整数 n: ")

    // 调用 fibonacci 函数，计算第 n 项及完整的斐波那契数列
    let (result, sequence) = fibonacci(n)

    // 输出第 n 项的值
    println("F(${n}) = ${result}")

    // 输出斐波那契数列的所有项
    println("斐波那契序列:")
    for (i in 0..sequence.size) {
        println("F(${i}) = ${sequence[i]}")  // 按格式输出每一项的值
    }

    return 0  // 返回 0 表示程序成功执行
}

---

代码详解

1. 存储中间结果：使用数组保存每一步计算的结果，避免重复运算。
2. Python 中，绘制斐波那契数列的图像并保存为本地文件。
3. Cangjie 实现输出整个斐波那契序列，帮助学生理解计算过程。

---

示例执行

示例 1：

输入：
n = 5
输出：
F(5) = 5

示例 2：

输入：
n = 10
输出：
F(10) = 55

---

四、图形展示

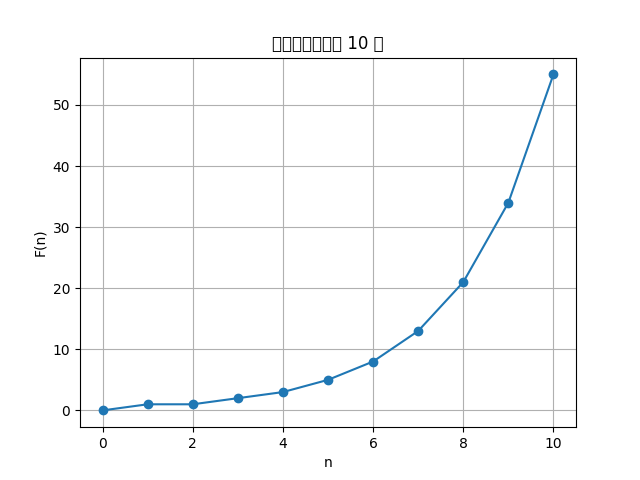
以下代码展示了斐波那契数列的前 10 项，并保存为 fibonacci_sequence.png：

plot_fibonacci_sequence(10)

生成的图像如下：

---

小结

通过这道斐波那契数列的题目，学生学习了动态规划的思想，并理解了如何使用编程优化递归算法。动态规划是一种重要的算法思想，常用于解决多阶段决策问题。

---

上一篇： 「Mac玩转仓颉内测版49」小学奥数篇12 - 图形变换与坐标计算

下一篇： 「Mac玩转仓颉内测版51」基础篇13 - 高阶函数与闭包

---

作者：SoraLuna 链接：https://www.nutpi.net 來源：坚果派 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

---